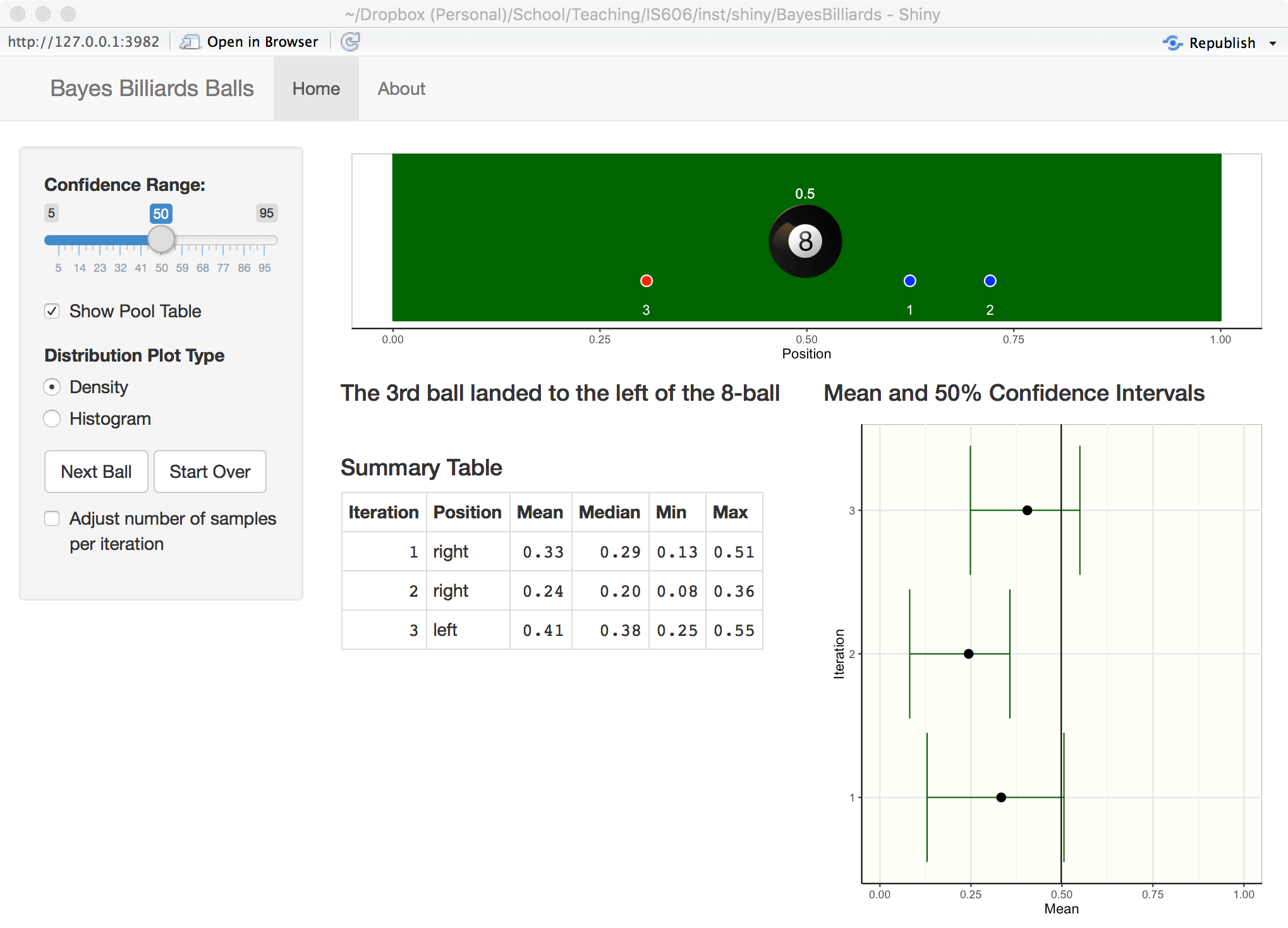
Consider a pool table of length one. An 8-ball is thrown such that the likelihood of its stopping point is uniform across the entire table (i.e. the table is perfectly level). The location of the 8-ball is recorded, but not known to the observer. Subsequent balls are thrown one at a time and all that is reported is whether the ball stopped to the left or right of the 8-ball. Given only this information, what is the position of the 8-ball? How does the estimate change as more balls are thrown and recorded?
You can run the app from RStudio’s shinyapps.io service at jbryer.shinyapps.io/BayesBilliards.
The Shiny App is included in the DATA606 package on Github and can be run, once installed, using the DATA606::shiny_demo('BayesBilliards') function.
Or, run the app directly from Github using the shiny::runGitHub('DATA606', 'jbryer', subdir='inst/shiny/BayesBilliards') function.
Source code is located here: https://github.com/jbryer/DATA606/tree/master/inst/shiny/BayesBilliards