My son has been learning Python and wanted to know how many rounds does it take, on average, for someone to win the game of war. If you are not familar with the game, it is a two player game where each player gets half a deck of cards (26). For each round the player puts down their top card. Whoever has the higher card gets both cards. In the instance where there is a tie, each player puts down three more cards and flips the fourth card. The player with the higher card gets all the cards put down (a total 10). If by chance there is a tie, they put down another three cards flipping the fourth. This is my attempt to solve this problem in R.
First I defined a function that performs a single round. Note that this function can be called recursively in the case there is a tie. The players cards are kept track in an integer vector p1 and p2 for player 1 and 2, respectively. It also returns an integer indicating who won that round.
#' Checks to see who wins the current round.
#'
#' This will compare the cards at position one. The winner gets both cards. If
#' there is a tie then the next three cards are put down and the fourth card
#' is compared. This is technically done recursively. The winner gets the
#' loosers five cards (the original, three put down, and the fourth is checked).
#'
#' The game ends when either of the players have no cards remaining.
#'
#' @param p1 cards for player 1.
#' @param p2 cards for player 2.
#' @return a list with three elements:
#' * `winner` - either a 1 or 2 for who won the round.
#' * `player1` - cards remaining for player 1.
#' * `player2` - cards remaining for player 2.
check_cards <- function(p1, p2) {
winner <- 0
if(length(p1) == 0) {
winner <- 2
} else if(length(p2) == 0) {
winner <- 1
} else {
if(p1[1] == p2[1]) {
# print('Entering a war!')
if(length(p1) < 5) {
p1 <- integer()
p2 <- c(p2, p1)
winner <- 2
} else if(length(p2) < 5) {
p1 <- c(p1, p2)
p2 <- integer()
winner <- 1
} else {
winners_cards <- c(p1[1:min(length(p1), 4)],
p2[1:min(length(p2), 4)])
result <- check_cards(p1[min(length(p1), 5):length(p1)],
p2[min(length(p2), 5):length(p2)])
if(result$winner == 1) {
p1 <- c(result$player1, winners_cards)
p2 <- result$player2
winner <- 1
} else if(result$winner == 2) {
p1 <- result$player1
p2 <- c(result$player2, winners_cards)
winner <- 2
}
}
} else if(p1[1] > p2[1]) {
p1 <- c(p1[-1], p1[1], p2[1])
p2 <- p2[-1]
winner <- 1
} else if(p2[1] > p1[1]) {
p2 <- c(p2[-1], p2[1], p1[1])
p1 <- p1[-1]
winner <- 2
} else {
stop('Should not be here. What happend?!')
}
}
return(list(
player1 = p1,
player2 = p2,
winner = winner
))
}Next I defined a function that will initiate a game of war. It has a while loop calling check_cards until one player has no more cards or max_games is reached therefore calling a draw.
#' Initiate a game of war.
#'
#' @param cards a vector representing the cards. The default assumes a typical
#' deck of 52 cards.
#' @param print how often should the function print the status of how many
#' cards each player has. Set to 0 to don't print any updates.
#' @param max_games the maximum number of games to try before it is considered
#' a draw.
#' @return a list with four elements:
#' * `games` - number of rounds it took for a player to win.
#' * `winner` - 0 for a draw, 1 if player 1 won, 2 if player 2 won.
#' * `p1_cards` - a numeric vector with the number of cards player 1 had after each round.
#' * `p2_cards` - a numeric vector with the number of cards player 2 had after each round.
play_war <- function(cards = rep(1:13, 4),
print = 0,
max_games = 2000) {
deal <- sample(length(cards), length(cards) / 2, replace = FALSE)
player1 <- cards[deal]
player2 <- cards[-deal]
games <- 0
p1_cards <- integer(max_games)
while(length(player1) > 0 & length(player2) > 0 & games < max_games) {
result <- check_cards(player1, player2)
player1 <- result$player1
player2 <- result$player2
p1_cards[games + 1] <- length(player1)
if(length(player1) == 0 | length(player2) == 0) {
break;
}
if(length(player1) + length(player2) != length(cards)) {
stop(paste0('No longer `have ', length(cards), ' cards! ',
(length(player1) + length(player2))))
}
games <- games + 1
if(print > 0) {
if(games %% print == 0) {
print(paste0('Game ', games, ':',
' Player 1 cards: ', length(player1), '; ',
' Player 2 cards: ', length(player2)))
}
}
}
winner <- 0
if(length(player1) == 0) {
winner <- 2
} else if(length(player2) == 0) {
winner <- 1
}
return(list(games = games,
winner = winner,
p1_cards = p1_cards,
p2_cards = length(cards) - p1_cards))
}We can now play a single game of war. Here print = 25 so the function will print the card status every 25 rounds.
play_war(print = 25)$games## [1] "Game 25: Player 1 cards: 19; Player 2 cards: 33"
## [1] "Game 50: Player 1 cards: 18; Player 2 cards: 34"
## [1] "Game 75: Player 1 cards: 29; Player 2 cards: 23"
## [1] "Game 100: Player 1 cards: 34; Player 2 cards: 18"
## [1] "Game 125: Player 1 cards: 29; Player 2 cards: 23"
## [1] "Game 150: Player 1 cards: 28; Player 2 cards: 24"
## [1] "Game 175: Player 1 cards: 9; Player 2 cards: 43"
## [1] "Game 200: Player 1 cards: 18; Player 2 cards: 34"
## [1] "Game 225: Player 1 cards: 43; Player 2 cards: 9"## [1] 229Let’s find out how many rounds it takes to win. Here we will play 10,000 games of war.
n_games <- 10000
war_games <- list()
for(i in seq_len(n_games)) {
# set.seed(i) # Used to track down issues and debug
war_games[[i]] <- play_war(print = 0)
}
plays_to_win <- sapply(war_games, FUN = function(x) { x$games })First we’ll see if there are any draws (unlikely with max_games = 2000).
draws <- which(plays_to_win == 2000)
sum(plays_to_win == 2000)## [1] 0Now let’s see what the mean, median, and distrubtion of rounds is.
hist(plays_to_win,
main = 'Histogram of Number of Plays to Win Game of War',
xlab = 'Number of Plays')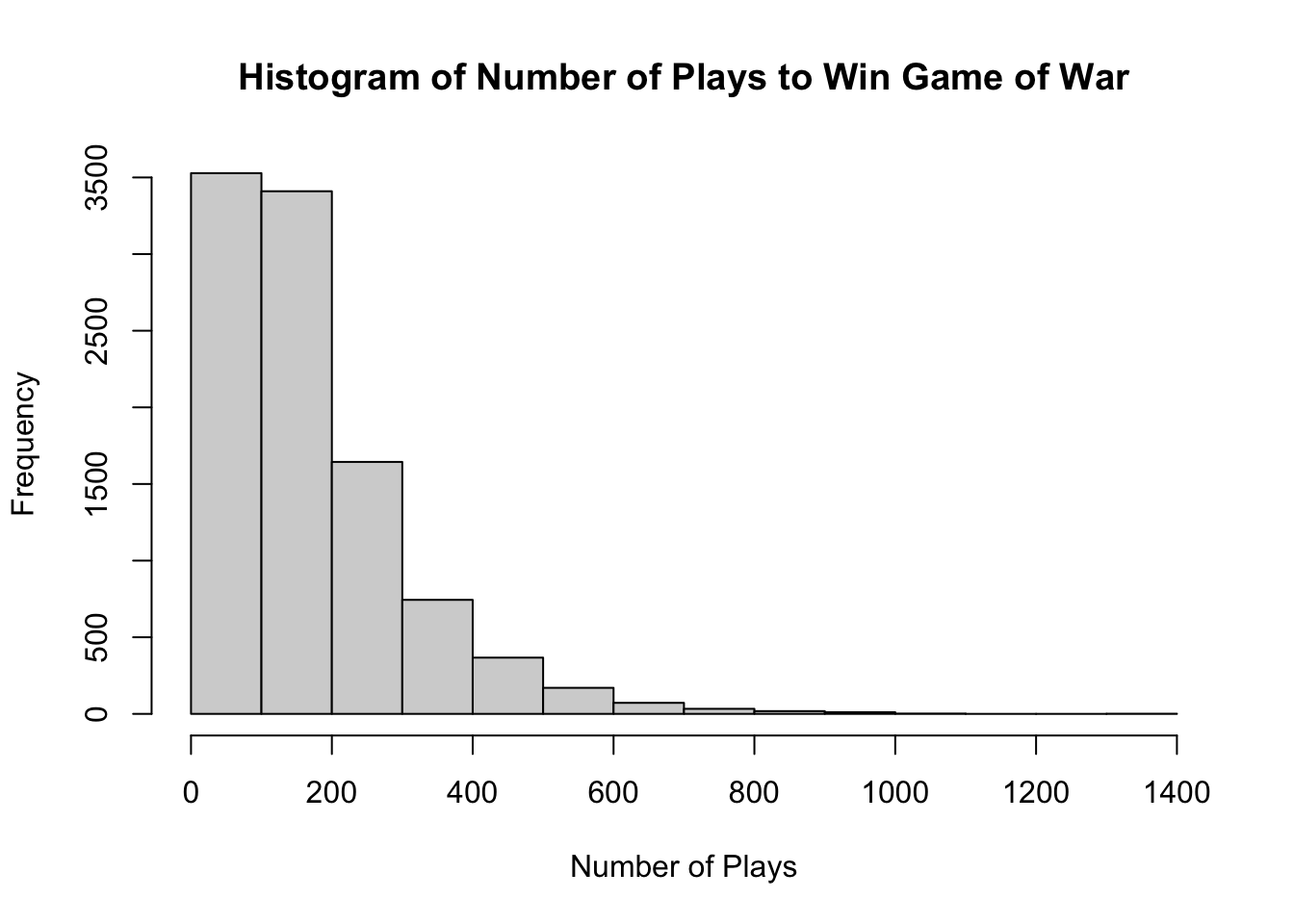
mean(plays_to_win)## [1] 173.6619median(plays_to_win)## [1] 135min(plays_to_win)## [1] 9max(plays_to_win)## [1] 1381